Dynamic Programming(동적 계획법, 다이나믹 프로그래밍)
응용 수학자 리차드 벨만(Richard Bellman)이 1953년에 고안한 알고리즘
큰 문제를 간단한 여러 개의(작은) 문제(Overlapping Subproblem)로 나누어 해결한 결과를 저장해뒀다가 나중에 큰 문제의 결과와 합하여 풀이하는 알고리즘
즉, 이미 해결한 (작은) 문제의 결과는 저장해 두었다가 다시 계산하지 않도록 하는 알고리즘
<다이나믹 프로그래밍의 조건>
- 부분 하위 문제(Overlapping Subproblem; 중복 부분 문제)
동일한 작은 문제를 반복적으로 해결
- 최적 부분 구조(Optimal Substructure)
큰 문제를 작은 문제로 나눌 수 있으며, 작은 문제의 답을 모아서 큰 문제를 해결
| Algorithm | 특징 | 대표적인 문제 |
| 다이나믹 프로그래밍 | - 최적 부분 구조 - 부분 하위 문제 |
- 피보나치 수열 - 다익스트라 알고리즘 |
| 분할 정복 | - 최적 부분 구조 - 탐욕 선택 |
- 퀵 정렬 |
| 그리디 알고리즘 | - 최적 부분 구조 | - 동전 문제 - 다익스트라 알고리즘 |
대표적인 다이나믹 프로그래밍의 예 : 피보나치 수열 문제
피보나치 수열의 점화식 : Fibo[i] = Fibo[i-1] + Fibo[i-2]
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...
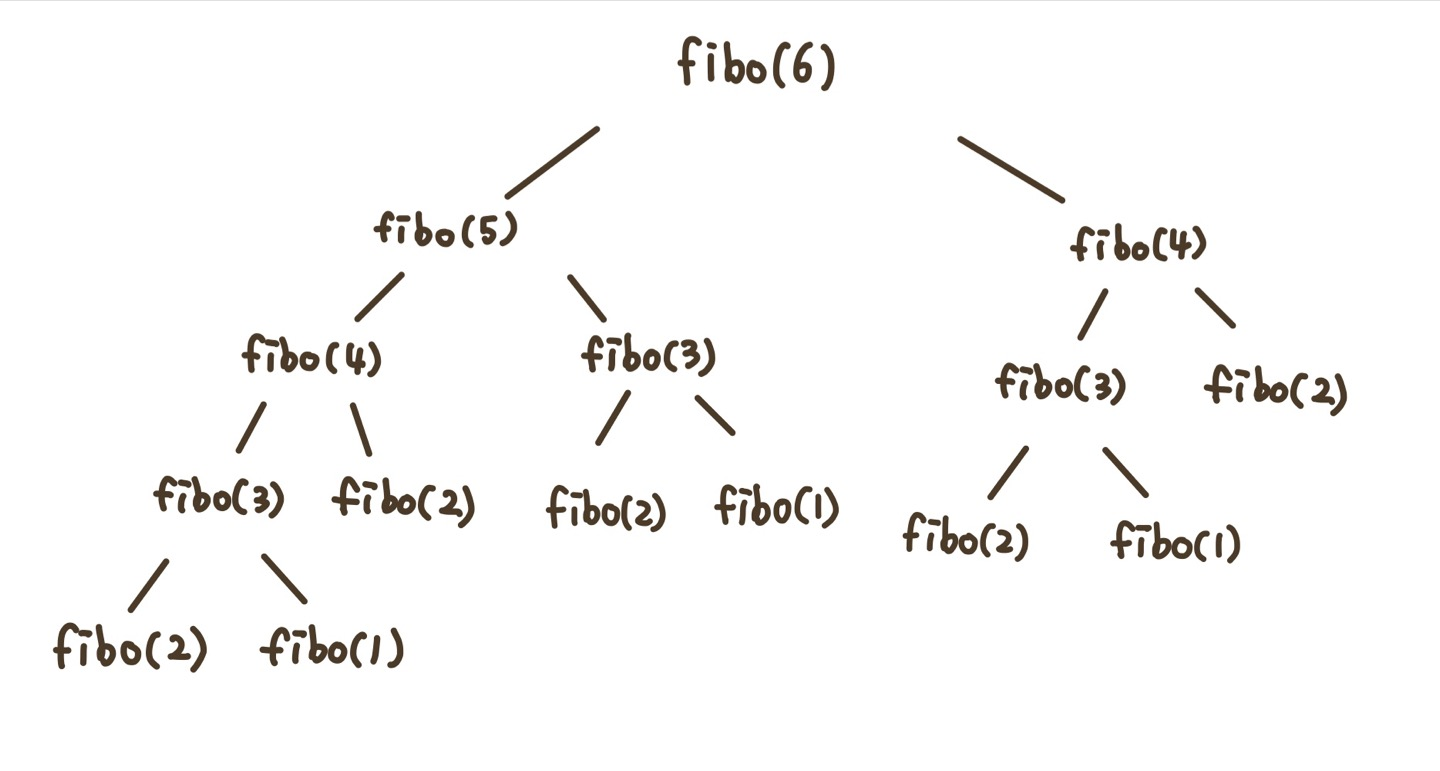
예를 들어 6번째 피보나치 수열을 구한다고 할 때, 6번째 값을 구하기 위해 15번의 함수 호출을 진행해야 한다.
즉 Fibo[6]를 구하기 위해서는 Fibo[5]와 Fibo[4]를 구해야하고 Fibo[5]를 구하기 위해서는 Fibo[4]와Fibo[3]을 구해야한다.
이미 진행했던 연산임에도 Fibo[4], Fibo[3], Fibo[2], Fibo[1] 들은 중복으로 연산한다.
이러한 것을 부분 하위 문제(Overlapping Subproblem; 중복 부분 문제)라 한다.
따라서 반복적으로 연산을 막기 위해 Fibo[4], Fibo[3], Fibo[2], Fibo[1] 처럼 이미 호출된 적 있는 함수들은 따로 별도의 메모리에 값을 저장해 같은 문제를 호출하면 다시 계산하지 않고 바로 결과 값을 가져오도록 한다.
'Study > Algorithm' 카테고리의 다른 글
| [Algorithm] LIS(Longest Increasing Subsequence; 최장 증가 부분 수열) (0) | 2022.03.14 |
|---|---|
| [Algorithm] Brute Force (브루트 포스) (0) | 2022.03.09 |
| [Algorithm] 이진 탐색(Binary Search, 이분 탐색, 이진 검색) (0) | 2021.10.11 |
| [Algorithm] LCS (최장 공통 부분 수열, 최장 공통 부분 문자열) (0) | 2021.10.03 |
| [Algorithm] 점근 표기법, 빅오 표기법(big-O notation) (0) | 2021.08.30 |


댓글