문제
이 문제는 아주 평범한 배낭에 관한 문제이다.
한 달 후면 국가의 부름을 받게 되는 준서는 여행을 가려고 한다. 세상과의 단절을 슬퍼하며 최대한 즐기기 위한 여행이기 때문에, 가지고 다닐 배낭 또한 최대한 가치 있게 싸려고 한다.
준서가 여행에 필요하다고 생각하는 N개의 물건이 있다. 각 물건은 무게 W와 가치 V를 가지는데, 해당 물건을 배낭에 넣어서 가면 준서가 V만큼 즐길 수 있다. 아직 행군을 해본 적이 없는 준서는 최대 K만큼의 무게만을 넣을 수 있는 배낭만 들고 다닐 수 있다. 준서가 최대한 즐거운 여행을 하기 위해 배낭에 넣을 수 있는 물건들의 가치의 최댓값을 알려주자.
입력
첫 줄에 물품의 수 N(1 ≤ N ≤ 100)과 준서가 버틸 수 있는 무게 K(1 ≤ K ≤ 100,000)가 주어진다. 두 번째 줄부터 N개의 줄에 거쳐 각 물건의 무게 W(1 ≤ W ≤ 100,000)와 해당 물건의 가치 V(0 ≤ V ≤ 1,000)가 주어진다.
입력으로 주어지는 모든 수는 정수이다.
출력
한 줄에 배낭에 넣을 수 있는 물건들의 가치 합의 최댓값을 출력한다.
예제 입력 1 복사
4 7
6 13
4 8
3 6
5 12
예제 출력 1 복사
14
나의 코드
[Python(파이썬)]
import sys
input = sys.stdin.readline
n, k = map(int, input().split())
nlist = [list(map(int, input().split())) for _ in range(n)]
check = [0] * (k + 1)
for i in range(n):
w, v = nlist[i]
for j in range(k, w-1, -1):
check[j] = max(check[j], check[j-w]+v)
print(check[-1])
풀이
- DP 설명
[Algorithm] Dynamic Programming(동적 계획법, 다이나믹 프로그래밍)
Dynamic Programming(동적 계획법, 다이나믹 프로그래밍) 응용 수학자 리차드 벨만(Richard Bellman)이 1953년에 고안한 알고리즘 큰 문제를 간단한 여러 개의(작은) 문제(Overlapping Subproblem)로 나누어 해결..
young-library.tistory.com
큰 문제를 간단한 여러 개의(작은) 문제(Overlapping Subproblem)로 나누어 해결한 결과를 저장해뒀다가 나중에 큰 문제의 결과와 합하여 풀이하는 알고리즘인 DP(Dynamic programming)를 사용하여 푸는 문제이다.
- 예제의 구현을 그림으로 표현
4 7
6 13
4 8
3 6
5 12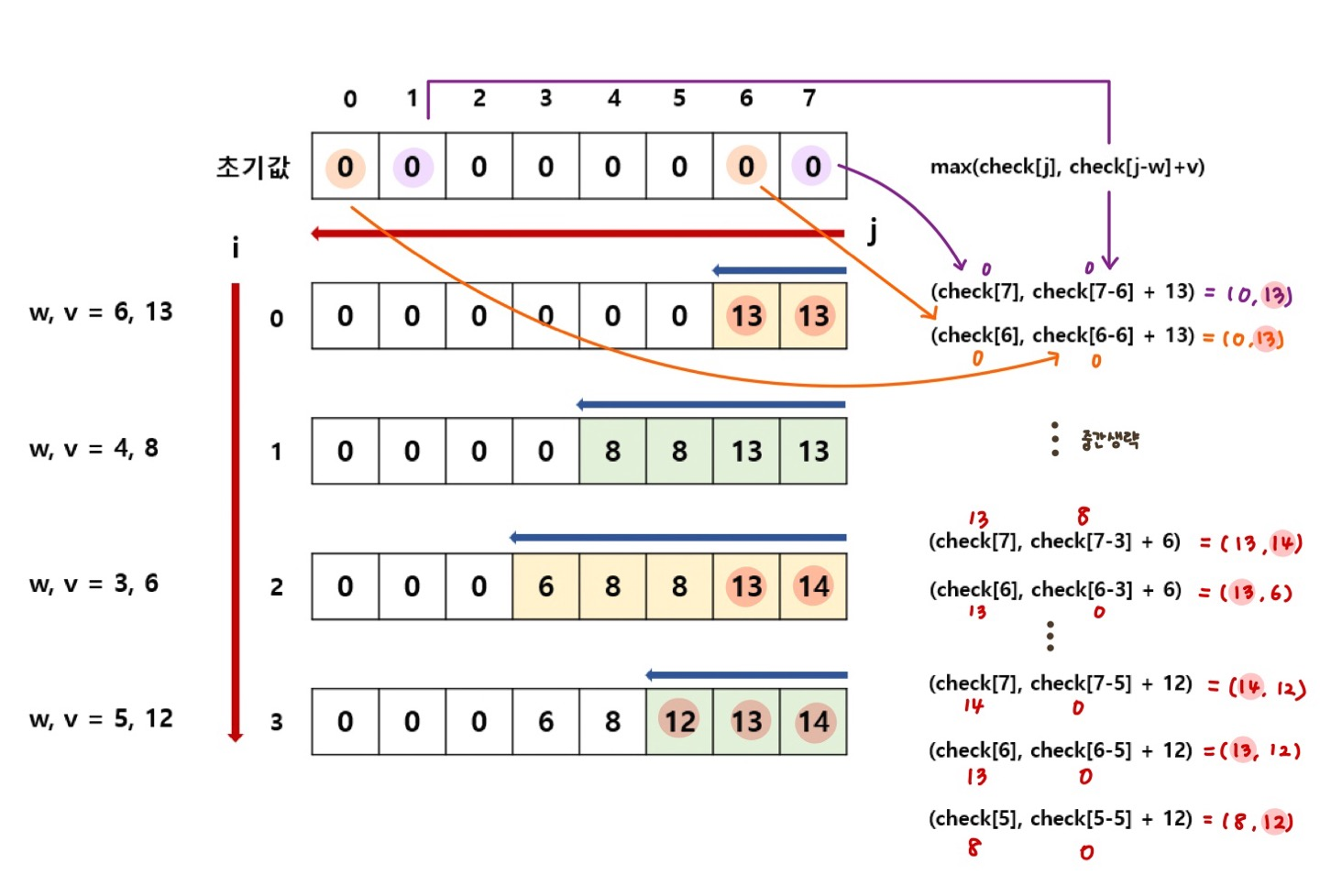
check 리스트에는 해당 인덱스의 무게에서 구할 수 있는 가중치의 최댓값을 저장한다.
i -> 0부터 (n(물품의 수) -1)까지
j -> k(준서가 버틸 수 있는 무게)부터 w(물건의 무게)까지 뒤에서 부터 계산
max(check[j], check[j-w]+v)
check[j] : 현재 물품 전까지의 j 무게 가중치 최댓값 -> 현재 물품은 가중치 최댓값에 포함되지 않음
check[j-w]+v : (j무게에서 현재 무게를 뺀) 무게의 가중치 최댓값 + 현재 들어올 물품 가중치 -> 현재 물품은 가중치 최댓값에 포함됨
-> 기존의 무게에서 현재 들어올 물품의 무게를 빼는 것이다. 그렇게 나온 무게(index)는 현재 들어올 물품과 함께 선택할 수 있는 물품의 무게가 되는 것이다. 해당 무게(인덱스)의 값은 기존 물품들의 가중치 최댓값이고 그 값에 현재 들어올 물품의 가중치를 더할 수 있다.
즉, max(현재 물품을 포함하지 않게 되는 가중치, 현재 물품을 포함한 가중치)가 된다.
위 그림을 보면서 예시를 보자
ex)
check = [0, 0, 0, 0, 8, 8, 13, 13] -> (6, 13), (4, 8) 2가지 물품을 계산한 가중치의 최대값이 저장되어있음
i = 2, j = 7
현재 물품 무게(w) = 3
현재 물품 가중치(v) = 6이라고 예시를 들면
check[7] = 현재 물품 가중치는 포함되지 않는 (6, 13), (4, 8) 2가지 물품을 계산했을 때 무게 7 가중치의 최댓값 = 13
check[j - w] = check[7 - 3] = check[4] = (6, 13), (4, 8) 2가지 물품을 계산했을 때 무게 4 가중치의 최댓값 = 8
-> 기존의 무게(7)에서 현재 들어올 물품의 무게(3)를 빼는 것이다. 그렇게 나온 4는 현재 들어올 물품(3)과 함께 선택할 수 있는 물품의 무게가 되는 것이다.
check[j - w] + v = check[7 - 3] + 6 = check[4] + 6 = 8 + 6 = 14
따라서 max(check[j], check[j-w]+v) = max(check[7], check[7-3] + 6) = max(13, 14) = 14가 된다.
j가 k부터 w까지 순서(왼쪽에서 오른쪽)로 이동하는 이유
j를 w(물건의 무게)부터 k(준서가 버틸 수 있는 무게)까지 오른쪽으로 이동하며 구하는 게 아니라 k(준서가 버틸 수 있는 무게)부터 w(물건의 무게)까지 왼쪽으로 이동하는 이유는 max(check[j], check[j-w]+v) 때문이다.
check[j-w]+v은check[j-w] (현재 물품은 가중치 최댓값에 포함되지 않고서) +v(현재 가중치를 더하는 것)이다. 하지만
앞에서부터 max(check[j], check[j-w]+v)를 구해서 오다 보면 이미 check[j-w]가 앞에서 check[j-w]+v 선택했다면 현재 물품의 가중치가 두 번 포함된 것이다.
ex)
3 5
4 2
3 4
1 5
- for j in range(w, k+1, 1) -> 틀린 코드
w(물건의 무게)부터 k(준서가 버틸 수 있는 무게)까지 오른쪽으로 이동하는 경우 check 리스트와 결과 출력
# w, v = 4, 2
[0, 0, 0, 0, 2, 2]
# w, v = 3, 4
[0, 0, 0, 4, 4, 4]
# w, v = 1, 5
[0, 5, 10, 15, 20, 25]
# 출력
25출력 결과 9가 나와야 하는데 25가 출력된다.
# 인덱스 무게의 최대 가중치와 최대 가중치일때 포함되는 물품의 무게들
[[0, 0], [5, (1)], [10, (1, 1)], [15, (1, 1, 1)], [20, (1, 1, 1, 1)], [25, (1, 1, 1, 1, 1)]]이유는 check[1]부터 check[j-w]+v 선택되어 1의 가중치인 5가 반복해서 더해지는 것이다.
- for j in range(k, w-1, -1)
k(준서가 버틸 수 있는 무게)부터 w(물건의 무게)까지 왼쪽으로 이동하는 경우 check 리스트와 결과 출력
# w, v = 4, 2
[0, 0, 0, 0, 2, 2]
# w, v = 3, 4
[0, 0, 0, 4, 4, 4]
# w, v = 1, 5
[0, 5, 5, 5, 9, 9]
# 출력
9
# 인덱스 무게의 최대 가중치와 최대 가중치일때 포함되는 물품의 무게들
[[0, 0], [5, (1)], [5, (1)], [5, (1)], [9, (3, 1)], [9, (3, 1)]]
따라서 현재 물품의 가중치가 여러 번 반복해서 들어가지 않도록 j는 k부터 w까지 왼쪽으로 이동해야 한다.
문제 출처
12865번: 평범한 배낭
첫 줄에 물품의 수 N(1 ≤ N ≤ 100)과 준서가 버틸 수 있는 무게 K(1 ≤ K ≤ 100,000)가 주어진다. 두 번째 줄부터 N개의 줄에 거쳐 각 물건의 무게 W(1 ≤ W ≤ 100,000)와 해당 물건의 가치 V(0 ≤ V ≤ 1,000)
www.acmicpc.net
'[Python] Baekjoon > Dynamic Programming(동적계획법)' 카테고리의 다른 글
| [Baekjoon(백준)] 2565 전깃줄 (0) | 2022.03.15 |
|---|---|
| [백준(Baekjoon)] 11053 가장 긴 증가하는 부분 수열 (0) | 2021.12.31 |
| [백준(Baekjoon)] 9251 LCS (0) | 2021.12.25 |
| [백준(Baekjoon)] 9095 1, 2, 3 더하기 (0) | 2021.12.25 |
| [백준(Baekjoon)] 11726 2*n 타일링 (0) | 2021.12.23 |




댓글